在概率问题中,生日悖论(Birthday Paradox)是一个非常经典的问题。简单描述,就是问一个教室中有多少学生时,至少有两个学生是同一天生日的概率会超过50%。答案是23个,这个数字和大多数人的直觉会有偏离,所以称之为“悖论”。计算的方法本篇博文就不叙述了,维基百科有很详细的说明。
生日悖论问题的本质是在有限个结果选择空间中,在时间上或者空间上随机事件出现重复结果的问题。生日悖论目前被应用于Hash函数的设计和研究中。
最近在网上搜到了一篇叫做《A Birthday Attack on Roulette》的文章。此文没有正式发表,不过作者把文章挂到了arxiv.org上。文章写于2013年,作者是一位印度裔的计算机系教授。文章很简单,主要在论述将生日悖论应用于轮盘(Roulette)赌局中,可以得到一种大于50%赢的概率的下注方法。
美式轮盘赌局一共有38个数字,1到36,加上0和00。押注的方法有多种,文章的方法是下注在某一局之前连续7局开出的数字上,长期赢的概率是大于50%的。这种下注方法的核心计算思想就是在连续n个赌局产生的数字至少有两个数字重复的概率,计算可以得出n=8的时候,这个概率大于50%。具体计算的步骤就不详述了,和生日悖论类似,不清楚的朋友可以参照文章。
到这里你可能会很有兴趣,如果一个下注方法赢的概率是大于50%的,那理论上我们只要屁股可以在赌桌前坐的够久,那一定会盈利。可以准备好行李买机票去拉斯维加斯或者澳门了。
去拉斯维加斯之前得先来验证一下,我写了个小程序来模拟一下这种押注方法(python程序见附录)。程序模拟10万次赌局,每次都下注在前7局开出的数字上,为了简化和清晰对比,不加入赔率,只算赢的概率。满怀希望地看一下结果,发现10万局赢的概率只有0.18584,说好的大于50%呢?根据文章,下注的数字越多,比如10,或者12,那赢的概率就会越大。那再看看我的程序模拟结果。
| 下注数字数 | 赢的概率 |
|---|---|
| 8 | 0.20827 |
| 9 | 0.23856 |
| 10 | 0.26242 |
| 11 | 0.28779 |
| 12 | 0.31475 |
| 13 | 0.34368 |
现实很残酷,哪里有50%嘛,一定是哪里出错了。的确有地方出错了,这个错误得回到生日悖论的问题上。文章中有一个从生日悖论中得出的重要的推论,我直接引用如下。
Equivalently, the Birthday Paradox suggests that if there are 22 randomly chosen people in a room with distinct birthdays and another randomly chosen person is added to the mix then the probability that the last person has the same birthday as one of the other 22 people is greater than 0.5.
这个推论的说法是如果房间中有22个随机选取有不同生日的人,第23个人进入这个房间此人与其他22人有相同生日的概率超过0.5。其实想一想,这个推论是不成立的,它不等同于一个房间中23人至少有两个人的生日会相同的概率,因为前者不包含有超过两个人生日为同一天的概率。要纠正这个错误,就要把distinct的条件去掉,而且也不能保证第23个人的生日与其他22个人中的至少一人相同,因为生日悖论的概率中已经涵盖了其他22人中有人生日相同的情况。
但其实上面的这个错误还不能算一个大错误,最大的毛病出自问题建模中的谬误。忽略上面这个错误,按照作者的思路,下面两个问题是等价的。
问题1:一个房间中23个人至少有两人的生日是同一天的概率。
问题2:一个房间中有22个人,又来了第23个人进入房间,这23个人至少有两人是同一天的概率。
这两个问题确实是等价的,因而作者直接把问题2应用于轮盘游戏中,他把房间中的22个人看做为当前赌局之前已开出数字的22个赌局,他们各自的生日即为前22场转出的数字,第23个人即为当前的赌局。这里将这个应用过程描述为问题3。
问题3:一个房间中有22个人,每次从房间出来一个人,报出自己的生日,记录下来,直至房间中所有人都出来。这时来了第23个人,此人的生日与其他22人的生日放在一起后至少有两个人的生日相同的概率。
精确的问题应该是第23人的生日与其他人的生日放在一起后他的生日与至少其他一人生日相同的概率。这里因为假设已经忽略了第一个错误,所以描述为问题3的说法。
最大的逻辑谬误就在问题2到问题3的转化。这两个问题是有本质差别的,在问题2中,房间中的22个人的生日是未知的,有很多种可能性;而在问题3中,在计算第23个人的生日加入进来后的概率时,这22个人的生日是确定的。就差了这么一点,算出的结论是截然相反的。
当作者将轮盘游戏连续8局当做一个整体计算至少两个数字重复的概率时,这个问题就是问题2的模式;而给定前7局的开球结果,计算第8局的数字时,这个问题就是问题3的模式(精确模式)。其实作者计算出的是押注连续8局中至少有两个重复数字的概率;很可惜,现实生活中的轮盘赌局是后一种情况,你只能下注当前局。
那模拟出来的结果到底是个什么情况?先看一下下面的图吧。
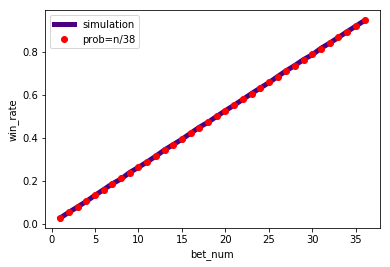
图中红色点绘制的是n/38的曲线,代表的就是在一局中我随便下注n个不同的数字会赢的概率。可以看出按照文章的下注方法和随机下注,其实没什么差别。我模拟的过程有细微差别,就是前7局可能会出现相同的数字,但从结果上差别非常微小。
文章中生日悖论应用于轮盘赌局的错误就论证完了。这件事情其实反映了一个非常典型的现象,在概率问题的建模中,问题转换中的逻辑错误常常会发生,而且会非常隐蔽,以致精通概率的人士们也会经常掉到坑里。
我根据这位教授的履历大概估计了一下,他在62岁左右写了这篇文章,为啥年纪这么大了还在研究赌博呢?
附录:python程序
import random
import matplotlib.pyplot as plt
numbers = list(range(-1, 37)) # -1 represents 00
win_rate = {}
for num_bet in range(1, 37):
bet_set = []
for i in range(0, num_bet):
bet_set.append(random.randrange(-1, 37))
num_run = 100000
num_win = 0
for i in range(0, num_run):
win_number = random.randrange(-1, 37)
if win_number in bet_set:
num_win = num_win + 1
else:
bet_set.pop(0)
bet_set.append(win_number)
win_rate[num_bet] = num_win*1.0/num_run
x = win_rate.keys()
sim = win_rate.values()
theo = []
for n in x:
theo.append(n * 1.0 / 38)
line1, = plt.plot(x, sim, label='simulation', color='Indigo', linewidth=5)
line2, = plt.plot(x, theo, 'o', label='prob=n/38', color='red')
plt.legend(handles=[line1, line2], loc='best')
plt.xlabel('bet_num')
plt.ylabel('win_rate')
plt.show()